Due. Tre. Cinque. Sette. Undici. E così via, all’infinito. Tutti i numeri sono uguali davanti alla matematica, ma qualcuno è più uguale. Si tratta, nomen omen, dei numeri primi, quelli dotati di due proprietà facili da comprendere anche per i profani, e innocue solo all’apparenza: essere maggiori di uno ed essere divisibili soltanto per sé stessi e per uno. Quindi, per l’appunto, il due, il tre, il cinque, il sette e via bellamente computando. I numeri primi ricoprono un ruolo decisamente importante all’interno della matematica, e in particolare, un po’ tautologicamente, nella cosiddetta teoria dei numeri, la branca che si occupa dello studio delle proprietà dei numeri interi.
Ciò che rende i numeri primi così interessanti agli occhi degli scienziati è, anzitutto, il fatto è che con essi si costruiscono – tramite la moltiplicazione – tutti gli altri numeri, in modo per di più univoco. Per questo, e per molti altri motivi, come vedremo tra poco, i numeri primi sono stati (e sono tuttora) oggetto di studio matto e disperatissimo da parte della comunità dei matematici. Nei secoli, gli studiosi hanno cercato di sviscerarne tutte le proprietà, decodificare le leggi che regolano la loro disposizione e comprendere come generarne sempre di più grandi. Ma l’interesse per i numeri primi va anche oltre la matematica pura: sui numeri primi sono basati, tanto per fare un esempio, molti dei metodi crittografici impiegati nell’ambito della sicurezza informatica e diversi algoritmi per la generazione di numeri (pseudo)casuali.
La storia di numeri primi
La prima “testimonianza” della definizione del concetto di numero primo è da datarsi addirittura al Paleolitico superiore: sull’osso di Hisango, un reperto osseo datato a circa 20mila anni fa (più precisamente il perone di un babbuino) compaiono dei segni che sono stati interpretati come la rappresentazione dei numeri primi compresi tra 10 e 20. Un’evidenza più chiara, e tardiva, è quella del papiro di Rhind, il più esteso documento egizio di argomento matematico giunto fino a noi, che contiene diverse espansioni in frazioni dei numeri nella forma 2⁄n, il che fa presupporre che gli autori fossero a conoscenza dell’esistenza dei numeri primi.
La formalizzazione di Euclide
La prima formalizzazione rigorosa si deve, però, a Euclide, che nei suoi Elementi enuncia, tra le altre cose, il teorema dell’infinità dei primi e la dimostrazione della possibilità di scomporre ogni intero positivo nel prodotto di numeri primi. Sempre di età classica è il cosiddetto crivello di Eratostene, il primo esempio di “setaccio” entro cui far passare tutti i numeri interi finché quello che rimane non sono solamente, per l’appunto, numeri primi. Il funzionamento del crivello è molto semplice: si scrivono tutti i numeri naturali a partire da 2 fino a un numero arbitrario e poi si cancellano i multipli di 2, poi di 3, poi di 5 e poi di 7. Facendolo per tutti i numeri da 2 a 100, per esempio, rimarranno nel setaccio soltanto numeri primi; con otto passaggi simili è possibile isolare tutti i numeri fino a 400, e con 168 setacciamenti si può arrivare fino al milione. Un sistema decisamente potente, insomma.
La riscoperta con Fermat, Marsenne ed Eulero
Per qualche ragione, successivamente l’interesse verso i numeri primi scemò fino a scomparire quasi del tutto dai lavori dei matematici. Per vederli tornare in auge bisogna attenere il diciassettesimo secolo, e in particolare i lavori del matematico Pierre de Fermat, del monaco Marin Mersenne e di Eulero, che studiarono la disposizione dei numeri primi, la possibilità di esprimerli come somma di interi e diverse altre congetture, alcune delle quali, tra l’altro, non sono state ancora dimostrate. Nell’Ottocento, i matematici – in particolare Bernhard Riemann, Adrienne Marie Legendre e Carl Gauss – si dedicarono allo studio della cosiddetta distribuzione asintotica dei primi, cioè la funzione che conta i primi minori o uguali a x, che culminò con la formulazione del teorema dei numeri primi, secondo il quale la funzione ha un andamento simile a x/ln(x).
L’era della crittografia
Arriviamo così ai giorni nostri. Negli anni settanta del Novecento, i numeri primi uscirono finalmente dal campo della matematica pura per entrare in quello dell’informatica, e in particolare della crittografia: molti algoritmi crittografici, infatti, si basano sulla difficoltà di scomporre numeri molto grandi in fattori primi. Per questo motivo, uno dei campi di ricerca attualmente più in voga è quello relativo all’individuazione di numeri primi molto grandi, servendosi di algoritmi sempre più raffinati e di processori sempre più potenti.
Come si cercano i numeri primi
Per studiare (e cercare) i numeri primi, i matematici, come dicevamo, passano i numeri interi attraverso “setacci virtuali” più e più volte, finché quello che rimane non sono solamente, per l’appunto, numeri primi. Già nel diciannovesimo secolo, questo processo di “setacciatura” ha prodotto tavole contenenti milioni di numeri primi, anche grazie all’invenzione, da parte del matematico tedesco Carl Friedrich Hindenburg, di uno strumento meccanico dotato di slider aggiustabili in grado di indentificare in un colpo solo tutti i multipli presenti in una pagina.
Oggigiorno, grazie all’enorme aumento della potenza computazionale che abbiamo a disposizione, i computer sono in grado di scovare miliardi di numeri primi in meno di un secondo: i matematici hanno così un’enorme mole di dati a disposizione per trovare pattern e regolarità (o irregolarità) sempre nuovi. Un esempio? La cifra finale: a parte il 2 e il 5, tutti i numeri primi terminano con 1, 3, 7 o 9; nel 1800 è stato dimostrato che queste possibili cifre finali sono ugualmente frequenti (ossia, se osserviamo per esempio i numeri primi fino a un milione, 250mila di essi – circa – termineranno con 1, 250mila con un 3, 250mila con un 7 e 250mila con un 9).
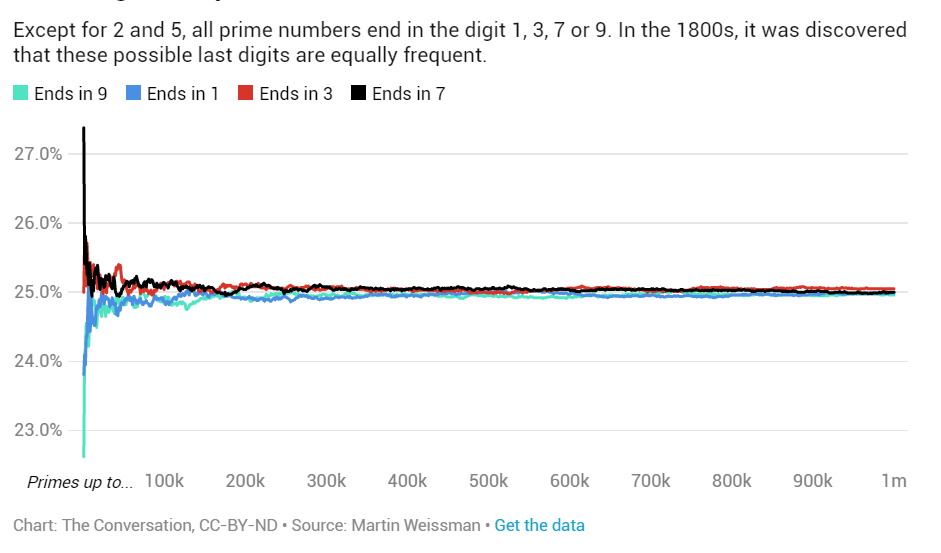
Solo di recente, grazie per l’appunto all’aumento dei numeri primi da studiare, due matematici di Stanford, Robert Oliver e Kannan Soundararajan, hanno scoperto un’irregolarità nella sequenza delle ultime cifre di numeri primi successivi: in altre parole, è molto più comune incontrare due numeri primi successivi che terminano con un 6 e un 9 (per esempio 26 e 29) che due numeri primi che terminano con un 7 e un 3. L’ovvia spiegazione del fenomeno è lasciata al lettore.
Cosa ancora non sappiamo
I numeri primi, bontà loro, continuano a serbare segreti che i matematici non sono ancora riusciti a comprendere. Tanto per fare qualche esempio, resta ancora da provare la cosiddetta congettura di Gilbreath, formulata dal matematico omonimo nel 1958. Volete provarci? Prendete carta e penna e scrivete un elenco di numeri primi consecutivi. Dopodiché sottraete il primo dal secondo, il secondo dal terzo, e così via, quindi scrivete il valore di tali differenze sotto il primo elenco. Ripetete ad libitum l’operazione: tutte le righe che avrete scritto – dice Gilbreath – dovrebbero cominciare con un 1. Nessuno, però, è mai riuscito a provarlo in modo stringente: al momento, la congettura è stata verificata fino a 1013.
E ancora: la congettura di Goldbach, che afferma che ogni numero pari maggiore di 2 può essere scritto come somma di due numeri primi (per esempio: 4 = 2 + 2; 20 = 13 + 7). O la congettura di Legendre, secondo la quale esiste sempre un numero primo compreso tra due quadrati perfetti consecutivi, e la congettura di Polignac, che afferma che per ogni numero intero positivo n esistono infiniti numeri primi consecutivi la cui differenza è pari a 2n (da notare l’ironia dei matematici: per n = 2 parlano di numeri primi cugini; per n = 3 parlano di numeri primi sexy). Insomma, c’è da divertirsi.
Mirabilia
Per chiudere in bellezza, una spigolatura di amenità e bizzarrie sui numeri primi.
Già nel diciottesimo secolo era nota una curiosissima serie di numeri primi: 31, 331, 3.331, 33.331, 333.331, 3.333.331, 33.333.331. E poi? Basta: il numero successivo, 333.333.331, non è primo, essendo uguale a 17 x 19.607.843.
Il numero primo 73.939.133 è molto particolare: rimuovendo una cifra per volta dalla destra si ottengono sempre e solo numeri primi: 7.393.913, 739.391, 73.939, 7.393, 739, 73, 7. È il numero primo più grande (tra quelli conosciuti finora, naturalmente) a godere di questa proprietà.
I numeri primi sono (ovviamente) infiniti. Ed è lecito pensare che, al loro crescere, aumenti anche la “distanza” tra un primo e l’altro; ovvero, in altri termini, che la differenza tra due numeri primi consecutivi cresca all’infinito. In realtà non è così: nel 2013 Yitang Zhang, matematico della University of New Hampshire, ha dimostrato la cosiddetta Bounded gaps conjecture, provando che esistono infinite coppie di numeri primi distanti tra loro meno di 70 milioni. Successivamente altri matematici hanno ulteriormente affinato tale dimostrazione, riducendo la differenza a 264.
Nel 1953, scarabocchiando dei numeri su un foglio di carta durante un meeting, il matematico polacco Stanislaw Ulam si rese conto che i numeri primi tendevano a disporsi in modo piuttosto particolare, allineandosi lungo le diagonali di una spirale. Che prese il nome, per l’appunto, di spirale di Ulam.

Altro che “solitudine”. Esistono anche i cosiddetti numeri primi gemelli: sono così definiti i numeri primi che differiscono tra loro per solo due unità, come per esempio 5 e 7, 11 e 13 e così via. Già nel 300 avanti Cristo, Euclide propose una congettura – al momento ancora non dimostrata – secondo la quale esisterebbero infinite coppie di numeri primi gemelli.
Il più grande numero primo noto al momento è 282589933 – 1 (meglio non scriverlo per esteso: è composto da 24.862.048 cifre). È stato scoperto nel 2018 da Patrick Laroche, della collaborazione Gimps (Great Internet Marsenne Prime Search).





Fantastico!
Il numero primo più grande del numero primo più grande noto, esiste e lo possiamo trovare tra i
numeri naturali con la proprietà invariantiva della sottrazione ma i tempi per verificare i risultati non sono compatibili con i nostri cicli di vita. Euclide con la formula 2*n+1 dimostra che esiste un numero primo più grande del primo più grande noto ma, nello stesso tempo, Il nuovo “inaccessibile ed irraggiungibile primo più grande di tutti i primi noti” con i primi precedenti, sono i nuovi primi la cui produttoria genera altri primi che a loro volta generano altri primi più grandi. Il risultato di ogni
operazione 2*n+1, comprenderà nuovi primi che con i vecchi genereranno una produttoria (2*n) che con +1 comprenderà nuovi primi ed in tal modo si è generato l’algoritmo che genera primi più grandi dei noti. Di certo sarà generato e sarà accessibile e raggiungibile il primo più grande dei primi noti ma nessun primo potrà mai essere il primo più grande di tutti i primi che si possano generare. Talete misura “l’inaccessibile e l’irraggiungibile” , Euclide genera e dimostra l’esistenza dell’inaccessibile ed irraggiungibile numero primo, Einstein, con la teoria della relatività e con E = m*c^2 dimostra che al crescere delle cifre che compongono il numero, (il numero primo più grande che conosciamo lo scriviamo con notazione potenza di due meno uno (2^82.589.933 -1) o con 24.862.048 cifre decimali riportabili su carta in Km di scrittura) lo stesso è inaccessibile ed irraggiungibile, aumenta lo “spazio” da analizzare e la quantità=spazio da comunicare con una velocità massima e che non si può superare: “la velocità della luce” . A numeri più grandi corrispondono spazi più grandi da percorrere, ne consegue che occorre più tempo per elaborare quel numero che, per quanto potrà essere grande, inaccessibile ed irraggiungibile Euclide ha dimostrato che esiste, Talete ha dimostrato che si può misurare ed Einstein ci ha fatto prendere atto e ci ha dimostrato che i nostri cicli di vita sono insufficienti per conoscere il
numero primo più grande del più grande noto.
Una risposta di quanti sono i primi contenuti in un numero dato ‘n, la si trova in una congettura di
Gauss (1792; pubblicato nel 1863) basata sull’analisi delle tavole dei numeri primi disponibili all’epoca. Dopo averla studiata, la risposta la cerchiamo nell’ipotesi di Riemann 1859.
https://pls.scienze.unipd.it/matematica/wpcontent/uploads/sites/3/2016/05/2015.05/mathesis.languasco.pdf. E’ uno dei problemi irrisolti fra i piu famosi della matematica e dimostrare questa ipotesi permetterebbe, https://https://www.bollatiboringhieri.it/libri/john-derbyshire-lossessione-deinumeri-primi-9788833926568/, di trovare una formula per generare l’elenco dei numeri primi e
conoscere quanti primi sono contenuti in un numero dato ‘n con ‘n anche molto grande.