Nel corso del convegno “Ricordando Daniela Furlan. Riflessioni sul fare scienze a scuola” (Spinea, 17 – 19 giugno 2015) Paolo Mazzoli, Direttore generale dell’Invalsi, l’Istituto Nazionale per la Valutazione del Sistema educativo di Istruzione e di formazione, si è confrontato con i docenti partecipanti sul sistema di valutazione della scuola italiana, raccogliendo critiche e suggerimenti e rispondendo ad alcune domande. Le risposte alla quarta domanda (mentre qui quelle alla prima: A cosa servono davvero i test INVALSI, alla seconda: Cosa indicano i dati raccolti con i teest INVALSI? e alla terza: L’INVALSI in terza media: valutiamo la scuola o l’alunno?)
di Paolo Mazzoli
4. Poiché tutti i test, anche quelli di matematica, sono formulati in forma scritta, secondo gli insegnanti rilevano soprattutto competenze di lettura. È davvero così?
Voi sostenete che con le prove si misurano le capacità di comprensione del testo e non le competenze matematiche; sulle implicazioni di questa affermazione non sono d’accordo con voi, ed il mio disaccordo si basa su diverse ragioni.
La mediazione linguistica è talmente trasversale ad ogni tipo di conoscenza che è difficilissimo, se non impossibile dire dove finisce la comprensione linguistica e dove comincia la comprensione matematica. Lavorando sulle prove di matematica ci siamo convinti che la comprensione della lingua fa anche parte della comprensione matematica oppure, per dirla in altri termini, che nella comprensione della lingua sono intrecciati aspetti logico-matematici.
Saper argomentare è fondamentale anche per la matematica; di conseguenza, i testi delle prove tengono conto del fatto che la posizione e la soluzione di un problema matematico implica anche una certa disinvoltura nella comprensione del testo. Potrebbe essere ragionevole, invece, l’obiezione di alcuni che pensano che le domande sono formulate in modo troppo difficile per il livello di comprensione dei bambini delle varie classi, e su questo si può discutere.
Ma le prove sono stati attentamente calibrate e sperimentate su un campione di studenti: delle 25-30 domande proposte ce ne sono alcune che sono calibrate al di sopra delle competenze medie, altre al di sotto e alcune che stanno nel mezzo. Perché sono state tutte inserite nelle prove nazionali? Perché lo scopo delle prove è quello di discriminare il più possibile. Dai pretest fatti sappiamo, ad esempio, che il 10-15% circa degli studenti è capace di rispondere anche a domande estremamente difficili. Non siete curiosi di sapere che nella vostre classi, già a sette anni, ci sono bambini particolarmente capaci, e sapere che accanto a questi ce ne sono altri che non rispondono a domande di difficoltà bassissima, cioè che sono al livello di bambini molto più piccoli? Non vi interessa conoscere le capacità dei vostri ragazzi, anche se sono molto fuori standard?
Dopo il pretest, quando presentiamo le domande alle scuole, noi controlliamo che vi sia un equilibrio tra le domande facili e quelle difficili, proprio per capire come nella classi sono distribuiti i ragazzi molto carenti, quelli che sono nella media e quelli che, pur essendo piccoli, sono già molto capaci. I risultati Invalsi possono dare queste informazioni in quanto i test pongono anche domande difficili. Se si facessero solo domande difficili, o solo domande facili, non si potrebbe dare alcuna informazione sullo spettro di capacità presenti in ogni classe. Poi, come agire didatticamente è un problema dell’insegnante.
Le prove rientrano nelle competenze richiamate dalle Indicazioni nazionali, e il livello di difficoltà massimo al quale spingersi viene individuato non sulla base delle opinioni degli esperti matematici ma in base ai risultati sul campo. I pretest ci dicono, per esempio, che un certo tipo di domanda formulata in quel modo (ma potrebbe anche essere formulata meglio) è risultata particolarmente difficile; e nell’analisi dei risultati si restituisce alla scuola un dato preso sul campo. Non interessa, e non si vuole, sapere se il teorema di Pitagora è più difficile di una “espressione a due piani”; si vuole sapere, all’atto pratico, come sono distribuite le capacità matematiche nella classe; e questo dovrebbe interessare anche gli insegnanti.
E poi, se fosse come dite voi, che cioè l’interpretazione linguistica fosse prevalente, noi dovremmo riscontrare una grossa correlazione tra i risultati della prova di matematica e quella di italiano. I dati dicono che c’è una certa correlazione, cioè che spesso i migliori in italiano sono anche i migliori in matematica, ma questo non vale per tutte le classi né per tutti gli studenti. Guardate questa tabella.
C’è un gruppo di 23 alunni che è particolarmente scarso in italiano ma ha ottimi risultati in matematica e, viceversa, c’è un gruppo di 12 alunni che è nettamente migliore in italiano che in matematica. Evidentemente alcune domande di matematica non hanno meno a che fare con l’interpretazione linguistica di quanto ci si aspetti.
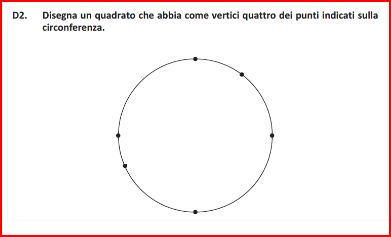
In quinta elementare sono state proposte domande grafiche. Guardate questa domanda, data quest’anno ai ragazzi di quinta primaria (vedi figura).
Disegna un quadrato che abbia come vertici quattro dei punti indicati sulla circonferenza. La risposta viene data col disegno, non con una parola o con una frase scritta, quindi la comprensione linguistica non è in gioco (o quasi). I nostri autori hanno discusso molto per decidere dove dovevano essere messi sulla circonferenza i punti da unire per disegnare il quadrato, ed è stata scelta la situazione in cui il quadrato da ottenere fosse risultasse ruotato rispetto alla sua posizione normale, con la base non parallela al bordo del foglio. A molti bambini faceva impressione pensare che un quadrato potesse anche essere “storto”; e voi capite bene quanto queste prove potrebbero orientare verso una maggiore flessibilità didattica.
A noi importava capire (e restituire agli insegnanti) la percentuale dei ragazzi che vedono soltanto le figure con le basi parallele alla terra, presentate come nelle figure dei libri. Certamente non rispondono così i ragazzi che imparano a riconoscere forme geometriche anche in figure che vengono buttate per aria e che cadono come cadono. Proprio in questo modo le prove invitano a sciogliere la rigidità e la banalità di certe convenzioni, stimolando una didattica più flessibile e intelligente.
(4-segue)
Credits immagine:Danielle Buma/Flickr CC